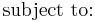Slater's condition
In mathematics, Slater's condition (or Slater condition) is a sufficient condition for strong duality to hold for a convex optimization problem. This is a specific example of a constraint qualification. In particular, if Slater's condition holds for the primal problem, then the duality gap is 0, and if the dual value is finite then it is attained.[1]
Mathematics
Given the problem
with  convex (and therefore a convex optimization problem). Then strong duality holds if there exists an
convex (and therefore a convex optimization problem). Then strong duality holds if there exists an  (where relint is the relative interior and
(where relint is the relative interior and  ) such that
) such that
 and
and [2]
[2]
If the first  constraints,
constraints,  are linear functions, then strong duality holds if there exists an
are linear functions, then strong duality holds if there exists an  such that
such that

 and
and [2]
[2]
Generalized Inequalities
Given the problem
where 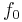 is convex and
is convex and 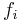 is
is 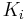 -convex for each
-convex for each  . Then Slater's condition says that if there exists an
. Then Slater's condition says that if there exists an  such that
such that
 and
and
then strong duality holds.[2]
References
- ^ Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 9780387295701.
- ^ a b c Boyd, Stephen; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 3, 2011.